前言
本文通过结合例题的形式来讲解贪心算法,可能需要实际动手做过题之后再看才能很好地理解。我个人认为,光看总结不做题是很难理解到题的本质的,所以还是做完题再看总结比较好。
也许这时候你自己也有了自己的理解和总结,阅读本文可以进行思想的交流和碰撞。
题目列表如下:由易到难
- 605. 种花问题
- 455. 分发饼干
- 122. 买卖股票的最佳时机 II
- 406. 根据身高重建队列
- 435. 无重叠区间
- 452. 用最少数量的箭引爆气球
- 763. 划分字母区间
- 135. 分发糖果
总结
贪心算法的核心适用条件:局部最优解可以拼凑出全局最优解。
贪心算法无非就是选择对当前局面最优的,或者说依靠当前局面就可以确定一个局部解,所以这一问题的关键在于所有局部解的组合是否最终能够得到全局最优解。
以605.种花问题为例,需要判断最多能种多少花,我们的贪心策略就是,只要当前可以种下花,那么就种下。许多个局部最优解(当前种下花)最终拼凑出了一个全局最优解(最多种多少花)。
455. 分发饼干也类似,每块饼干只给刚好能满足的或最接近满足的,每次的最优最终能拼出全局的最优。
再以122.买卖股票的最佳时机 II举例,需要赚最多的钱,由于本题在当天可以同时进行购买和出售,所以当天的操作不会影响到明天的操作。使用贪心算法即可,累加所有能赚钱的机会,就是全局最优的。
例如股价[1,2,4,5]的操作序列[买,卖买,卖买,卖],只要当天有得赚就进行购买和出售。而假如当天的操作会影响到明天,此时贪心算法可能就不适用了(当前的解实际上还取决于后续信息)。例如309. 最佳买卖股票时机含冷冻期,局部的最优解并不能拼凑出全局的最优解(当前的解会影响到后续,导致无法全局最优),此时就要从全局的角度去考虑问题了。
更复杂一些,如135. 分发糖果,此时全局最优是通过两次局部最优的贪心遍历得来的(题解),仍然是通过局部最优拼凑出全局最优。
而像763. 划分字母区间、435. 无重叠区间(题解)、452. 用最少数量的箭引爆气球这类的区间问题,总得来说也是贪心算法。依靠当前信息即可确定一个解,而不会受后续信息的影响。
最后再以一个个人认为能对贪心算法进行直观理解的题做结尾:406. 根据身高重建队列
在对身高进行升序排序之后,遍历到当前元素,我们就能够知道该元素所该在的最终位置,不论后续元素如何。因为对于空位置,即使不知道他该放入什么元素,但他身高一定是大于等于自己的(升序排序,后续未排入的元素的身高总归是大于等于自己的)。
可以通过手动模拟一下排列过程,结合代码进行理解。
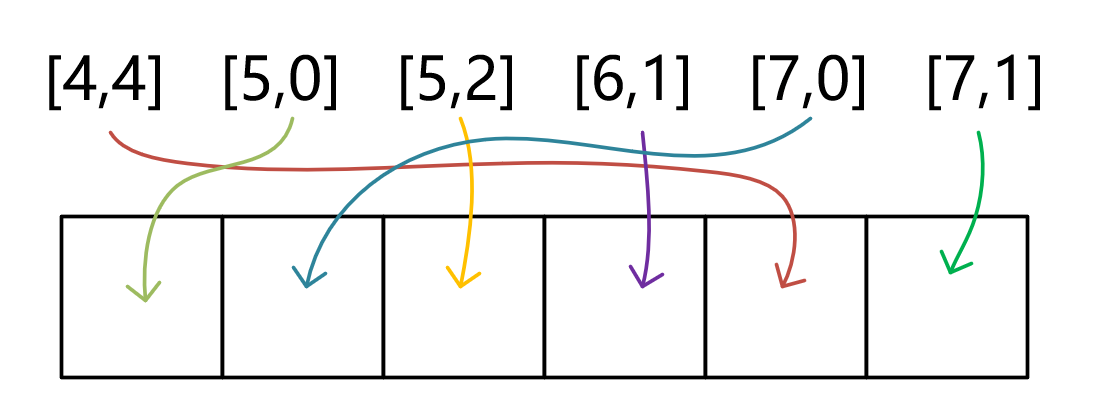
406.根据身高重建队列题解:
class Solution {
int EMPTY = -1;
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort(people.begin(), people.end(), [](auto& r, auto& l){
return r[0] < l[0];
});
vector<vector<int>> result(people.size(), {EMPTY, EMPTY});
for(int i = 0; i < people.size(); i++){
int count = people[i][1], k = 0;
while(count >= 0){
if(result[k][0] == EMPTY || result[k][0] >= people[i][0]){
count--;
}
k++;
}
result[k - 1] = people[i];
}
return result;
}
};
最后,我们都知道计算机是原子视角,如果不做额外的存储,它只能知道当前的东西是什么。更总结地说,我们只需要知道当前的信息和先前的信息(比如到目前为止的最大值最小值),就可以确定当前信息的解,而这个解不会受到后续信息的影响。
当然通常不会这么明显,需要自己做一些处理和分析,例如406. 根据身高重建队列。
