前言
In computer science, cycle detection or cycle finding is the algorithmic problem of finding a cycle in a sequence of iterated function values.
简单来说,就是在迭代中检测是否存在环路。迭代是计算机中最基本的一种执行模式,几乎任何程序都需要用到迭代(即循环)。环路检测就是应用在具有迭代结构的程序里,用于检测程序是否会在一个环路中死循环,或是用来检测图、链表或状态机等结构中是否含有环。
所以我们由此得出一个问题:如何判断是否有环,如果有环,环点(环的起点)在哪,环有多长?
算法原理
对于环的判断可以很容易得出一种算法,我们知道在环里绕圈圈必然会重复经过某个节点。所以我们记录下每个节点的信息,当出现节点信息重复的时候,就说明环存在。环点就是第一个检测到重复的节点,那么环长也能基于此计算出来了。
但是这样的算法有个致命的问题,当环非常长时,储存节点的空间开销就逐渐变得不可接受,有没有一种方法能够不记录这么多节点,就能够判断环呢?
所以就出现了我们今天的主角:Floyd’s tortoise and hare
Floyd 很形象的描述了他的算法 Tortoise and Hare,乌龟和兔子。实际上就是快慢指针的一种形象化表示。
那为什么快慢指针能解决这个问题呢,这基于这样一个前提:在环中,快的一方总会追上慢的一方,即在环中相遇。
接下来我们抛开麻烦的数学推导,用几张图形象地进行推理。
推理
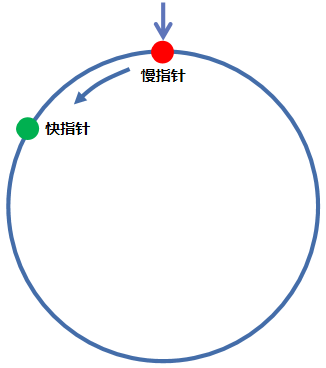
首先,我们假设整条链路都是一个环,如下图所示。快慢指针都在起点开始运动(快指针运动速度是慢指针的两倍),那么当慢指针走完一圈时,快指针刚好走了两圈,并且二者恰好在起点相遇。

那么我们加上一条直链会怎么样呢?如下图所示,当快慢指针共同经过一条直链后,从慢指针进入环点的这一刻来看,快指针已经从环点走出了一段距离。
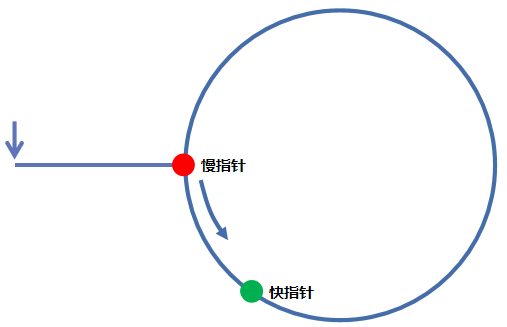
那么再回到我们的圆环模型,我们将环点当作起点,如下图。当他们在起点一起出发时,最终快指针会在起点追上慢指针。而当快慢指针一起经过一段直链之后,快指针多走了一段距离,所以最终快指针会在慢指针回到起点前就追上它。
于是我们得到一个结论:慢指针在环中至多走完一圈就会被快指针追上。
所以我们对于环的判断就变得简单了:
- 如果慢指针与快指针相遇,则存在环,且慢指针最多走完一圈
- 如果慢指针最终走向了某种形式的尽头,则无环(例如链表,无环则最终节点为
null)
我们确定了存在环,那么环长的判断就简单了:
- 记住当前节点信息,进行计数,最终回到该节点,就可以得到环长
那么环点如何确定呢?这时候需要进行一定的数学推导,但也十分简单。
如下图所示,我们标记三段距离:
- 起点到环点的距离
a - 慢指针在环内的移动距离
b - 相遇点到环点的距离
c
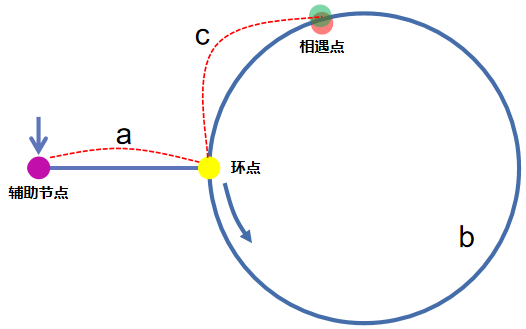
假设快指针在环内已经走了 n 圈,那么有关系 a + n*(b+c) + b = 2 * (a+b),即快指针路程是慢指针的两倍。
于是有 a = (n-1)(b+c) + c,也就表明 n-1 圈的环长加上 c 就是环点与起点的距离。实际上也表明慢指针再走过距离 a,最终会停在环点上(走过 n-1 圈还是在相遇点,再走过距离 c 就到了环点)。
但由于我们不知道圈数是多少,所以也无法确定何时停下来,这时候就需要引入一个辅助节点了。我们让辅助节点和慢指针一起移动,最终他们会在环点相遇(辅助节点走过距离 a 到环点,慢指针走过距离 a 也会停在环点),当他们相遇时,就可以计算出环点距离起点的距离了。
至此我们就解决了关于环的所有问题:
- 判断环是否存在
- 计算环长
- 确认环点
